A sphere is a solid bounded by a surface every point of which is equally distant from a fixed point.
(Alt.) When a semicircle with fixed diameter is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a sphere.
Euc. XI.D.14.
That fixed point is called the center of the sphere.
(Alt.) The center of the sphere is the same as that of the semicircle.
Euc. XI.D.16.
The straight line which joins any point of the surface with the centre is called a radius.
A straight line drawn through the centre and terminated both ways by the surface is called a diameter.
A spherical triangle is formed by the intersections of three great circles on the surface of a sphere - the sides of a spherical triangle are always arcs of great circles.
The figure bounded by those great circles and the center of the sphere is a trihedral angle.
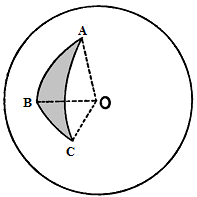
In spherical triangle ABC, arcs AB, BC, CA, and angles AOB, BOC, COA subtend the same number of degrees.
To find the relation between two sides of any spherical triangle and the angles opposite
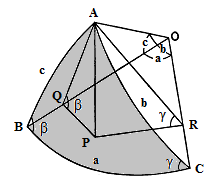
- Let ABC be a spherical triangle of a sphere of unit radius with center O.
- Draw line AP perpendicular to plane BOC and intersecting it at P.
Euc. XI.P.11
- Draw lines PQ, PR in plane BOC, perpendicular to OB, OC respectively.
Euc. I.P.12
- Then lines PQ, PR are perpendicular to line AP.
Euc. XI.D.3
- Therefore, triangles APQ, APR are right triangles with hypotenuses AQ, AR.
- Since line AP is perpendicular to plane BOC, planes
APQ, APR are perpendicular to plane BOC
Euc. XI.P.18
- Lines OB, OC are perpendicular to planes APQ, APR respectively.
Euc. XI.D.4
- Angles AQO, ARO are right angles. Euc. XI.D.3
- And triangles AQO, ARO are right triangles with hypotenuse OA.
- From (5), sin β = AP⁄AQ and
sin γ = AP⁄AR
- Therefore, sin β⁄ sin γ = AR⁄AQ.
- From (9), sin b = AR⁄OA and
sin c = AQ⁄OA
- Therefore, sin b⁄ sin c = AR⁄AQ.
- Rearranging (11) and (13), sin b⁄ sin β = sin c ⁄ sin γ.
By constructions analogous to steps (2) and (3) for vertices B, C, it follows that:
- sin a⁄ sin αsin b⁄ sin β = sin c ⁄ sin γ.