Create a sentence with the word "causes" in it.
Then the independent variable "causes" the dependent variable
Example
Independent: number of players on the DL list
Dependent: length of losing streak

If you begin collecting data on a variable that is continuous, such as heights, weights, temperatures, etc., if you take enough samples (collect enough data points), the population will usually be described by the Normal Distribution. That can be proven by something called the Central Limit Theorem, but the proof is a mathematical exercise best left to math geeks.
The Normal Curve is a function plotted in xy coordinates. The actual equation is complex and not necessary to learn. The key features of the normal distribution are as follows:

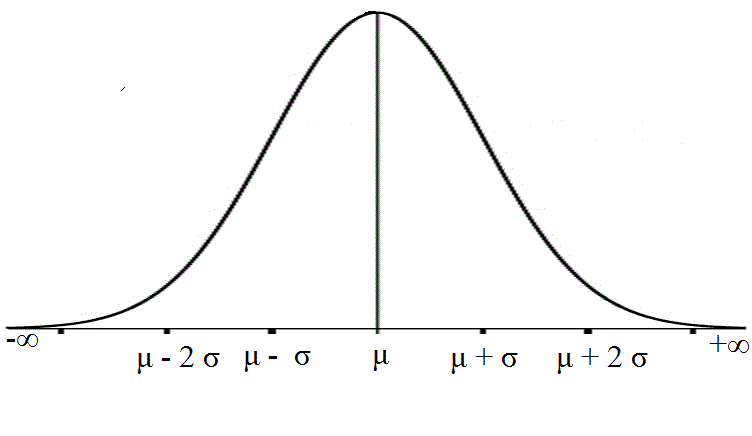
• It has the shape of a "bell" curve
• The curve is horizontally symmetric (the left half will match the right if folded over)
• The tails of the curve extend indefinitely and never actually touch the X axis
• The midpoint of the curve is the same as the arithmetic mean of the sample and is designated by μ (mu)
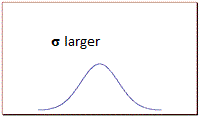
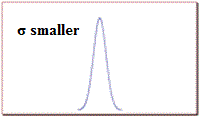
• A value named σ (sigma) is the same as the standard deviation of the sample. When σ is large, the curve is short and wide; when σ is small, the curve is tall and narrow.

The Normal Distribution is a continuous probability density function defined by the area under a portion of the Normal Curve. The total area under the curve is always 1, no matter what μ and σ are The thing that is important about the Normal Curve is not the value of any point on it. What is important is the area (distribution) under various portions of it.
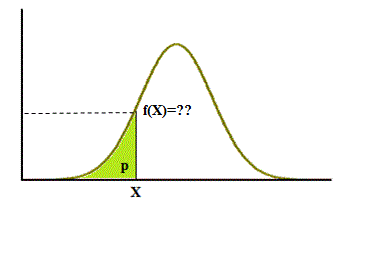
Some of the kinds of questions you can use the Normal Distribution to answer are as follows (use the above diagram):

• What is the probability that some value, A, is greater than X? (X < A < +∞)
• What is the probability that some value, A, is less than X? (-∞ > A < X)

Most problems using the normal distribution involve matching up and combining "slices" of area with the number of standard deviations of the mean. The mean (μ) and standard deviation (σ) are usually provided. Here's a diagram of the most important slices:

Using the above diagram, if the average (μ) of Major League pitchers' ERA's is and the standard deviation (σ) is , then:

• 50% of pitchers had an ERA less than
• If a pitcher is selected at random, the chance his ERA is greater than is 50%
• 34% of pitchers had an ERA between (μ - 1σ) and (μ)
• If a pitcher is selected at random, the chance his ERA is between (μ) and (μ + 1σ) is 34%

The following numbers are important to recognize in a problem:

2.5%	-∞ to μ - 2σ		μ + 2σ to +∞
5%	-∞ to μ - 2σ AND μ + 2σ to +∞
13.5%	μ - 2σ to μ - 1σ		μ + 1σ to μ + 2σ
16%	-∞ to μ - 1σ		μ + 1σ to +∞
32%	-∞ to μ - 1σ AND μ + 1σ to +∞
34%	μ - 1σ to μ		μ to μ + 1σ
47.5%	μ - 2σ to μ		μ to μ + 2σ
50%	-∞ to μ		μ to +∞
68%	μ - 1σ to μ + 1σ
84%	-∞ to μ + 1σ		μ - 1σ to +∞
95%	μ - 2σ to μ + 2σ
97.5%	-∞ to μ + 2σ		μ - 2σ to +∞

The mean batting average (μ) for the American League is now The standard deviation (σ) of the batting average for the American League is now 50% of the batters had batting averages greater than If you select a random batter, the probability his average is less than is 50% of the batters have averages GREATER THAN ??? A randomly selected batter has a ??? chance of having a batting average less than of the batters have averages BETWEEN ???