| λ(nm) | x̅(λ) | y̅(λ) | z̅(λ) | RGBlinear | luminance | RGBmin-max | RGB≥0 | R+G+B | clipped | scaled@1 | scaled@lum | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ** | ||||||||||||||||
Begin with physically measurable data, namely the wavelengths of visible light (λ).
The visible spectrum ranges from 390nm, perceived as violet, through indigo, blue, cyan, green, yellow, orange and red, at 830nm.
All human perceivable colors are a mixture of lights from each wavelength.
Quantification of human color perception of visual stimuli is carried out by measurement of XYZ tristimulus values, X(λ), Y(λ), Z(λ).
These are obtained by asking observers to "mix" 3 imaginary primary colors (X, Y and Z) to match pure (one wavelength) colors on the spectrum.
The XYZ primaries are mathematically derived, not physical, colors with the following properties:
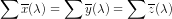 There are various CMFs, each of which produces a slightly different set of tristimulus values.
Many are available at http://cvrl.ioo.ucl.ac.uk/cmfs.htm
Real world visual output is rendered by the additive mixture of physically realizable RGB primaries,
not imaginary XYZ primaries.
With specification of RGB primaries and whitepoint in XYZ coordinates,
any set of XYZ values can be transformed into a set of RGB values via matrix multiplication.
For computer monitor screens, the RGB primaries are specified by
ITU-R Recommendation BT.709. This specification sets forth X,Y and Z values for each of these RGB primaries,
as well as an XYZ white point, D65 in this case. That recommendation refers to studio monitors and HDTV;
the same primaries are specified for sRGB, the color space that is used by Windows,
the Web and most image formats including JPEG.
The matrix for transforming XYZ to sRGB is:
There are various CMFs, each of which produces a slightly different set of tristimulus values.
Many are available at http://cvrl.ioo.ucl.ac.uk/cmfs.htm
Real world visual output is rendered by the additive mixture of physically realizable RGB primaries,
not imaginary XYZ primaries.
With specification of RGB primaries and whitepoint in XYZ coordinates,
any set of XYZ values can be transformed into a set of RGB values via matrix multiplication.
For computer monitor screens, the RGB primaries are specified by
ITU-R Recommendation BT.709. This specification sets forth X,Y and Z values for each of these RGB primaries,
as well as an XYZ white point, D65 in this case. That recommendation refers to studio monitors and HDTV;
the same primaries are specified for sRGB, the color space that is used by Windows,
the Web and most image formats including JPEG.
The matrix for transforming XYZ to sRGB is:
 The columns headed by RGBlinear display this transformation.
Note that the transformation matrix has negative terms, so negative RGB values are possible.
In fact, for reasons beyond the scope of this discussion, all spectral colors have at least 1 negative RGB value.
Since a negative amount of light cannot be visually supplied, these values must be further transformed.
Here, this is accomplished by finding the minimum value of RGBlinear, and subtracting it from
each of the values so that the minimum transformed value is now zero.
Results are shown in RGB≥0.
For linear RGB, the minimum amount of a primary that can be present is 0, and the maximum is 1.
So the RGB≥0 must be normalized. Three possibilities come to mind:
The columns headed by RGBlinear display this transformation.
Note that the transformation matrix has negative terms, so negative RGB values are possible.
In fact, for reasons beyond the scope of this discussion, all spectral colors have at least 1 negative RGB value.
Since a negative amount of light cannot be visually supplied, these values must be further transformed.
Here, this is accomplished by finding the minimum value of RGBlinear, and subtracting it from
each of the values so that the minimum transformed value is now zero.
Results are shown in RGB≥0.
For linear RGB, the minimum amount of a primary that can be present is 0, and the maximum is 1.
So the RGB≥0 must be normalized. Three possibilities come to mind:
 Finally, sRGB values are encoded as 8 bits, so the normalized RGB values are multiplied by 255 and rounded.
The results of the 3 scaling methods are displayed in the 3 right-hand columns.
Finally, sRGB values are encoded as 8 bits, so the normalized RGB values are multiplied by 255 and rounded.
The results of the 3 scaling methods are displayed in the 3 right-hand columns.
- Any human perceivable color can be described by a set of XYZ tristimulus values.
- XYZ tristimulus values are always positive
- Equal values of X, Y and Z produce achromatic colors (white → gray → black)
- The Y parameter determines the luminance of the color (separately derived from observer data)
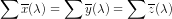 There are various CMFs, each of which produces a slightly different set of tristimulus values.
Many are available at http://cvrl.ioo.ucl.ac.uk/cmfs.htm
Real world visual output is rendered by the additive mixture of physically realizable RGB primaries,
not imaginary XYZ primaries.
With specification of RGB primaries and whitepoint in XYZ coordinates,
any set of XYZ values can be transformed into a set of RGB values via matrix multiplication.
For computer monitor screens, the RGB primaries are specified by
ITU-R Recommendation BT.709. This specification sets forth X,Y and Z values for each of these RGB primaries,
as well as an XYZ white point, D65 in this case. That recommendation refers to studio monitors and HDTV;
the same primaries are specified for sRGB, the color space that is used by Windows,
the Web and most image formats including JPEG.
The matrix for transforming XYZ to sRGB is:
There are various CMFs, each of which produces a slightly different set of tristimulus values.
Many are available at http://cvrl.ioo.ucl.ac.uk/cmfs.htm
Real world visual output is rendered by the additive mixture of physically realizable RGB primaries,
not imaginary XYZ primaries.
With specification of RGB primaries and whitepoint in XYZ coordinates,
any set of XYZ values can be transformed into a set of RGB values via matrix multiplication.
For computer monitor screens, the RGB primaries are specified by
ITU-R Recommendation BT.709. This specification sets forth X,Y and Z values for each of these RGB primaries,
as well as an XYZ white point, D65 in this case. That recommendation refers to studio monitors and HDTV;
the same primaries are specified for sRGB, the color space that is used by Windows,
the Web and most image formats including JPEG.
The matrix for transforming XYZ to sRGB is:  The columns headed by RGBlinear display this transformation.
Note that the transformation matrix has negative terms, so negative RGB values are possible.
In fact, for reasons beyond the scope of this discussion, all spectral colors have at least 1 negative RGB value.
Since a negative amount of light cannot be visually supplied, these values must be further transformed.
Here, this is accomplished by finding the minimum value of RGBlinear, and subtracting it from
each of the values so that the minimum transformed value is now zero.
Results are shown in RGB≥0.
For linear RGB, the minimum amount of a primary that can be present is 0, and the maximum is 1.
So the RGB≥0 must be normalized. Three possibilities come to mind:
The columns headed by RGBlinear display this transformation.
Note that the transformation matrix has negative terms, so negative RGB values are possible.
In fact, for reasons beyond the scope of this discussion, all spectral colors have at least 1 negative RGB value.
Since a negative amount of light cannot be visually supplied, these values must be further transformed.
Here, this is accomplished by finding the minimum value of RGBlinear, and subtracting it from
each of the values so that the minimum transformed value is now zero.
Results are shown in RGB≥0.
For linear RGB, the minimum amount of a primary that can be present is 0, and the maximum is 1.
So the RGB≥0 must be normalized. Three possibilities come to mind:
- Simple clipping of values greater that 1 to 1
- Scaling by division of all 3 RGB values based upon the maximum value
- Scaling of all 3 RGB values to retrieve the original luminance.
As per above, the luminance can retrieved from the Y parameters (from the inverse of the above XYZ to RGB matrix).
Namely, lum(R,G,B) = 0.212673R + 0.715152G + 0.072175B. Then: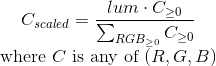 ,
,
 Finally, sRGB values are encoded as 8 bits, so the normalized RGB values are multiplied by 255 and rounded.
The results of the 3 scaling methods are displayed in the 3 right-hand columns.
Finally, sRGB values are encoded as 8 bits, so the normalized RGB values are multiplied by 255 and rounded.
The results of the 3 scaling methods are displayed in the 3 right-hand columns.